Habitualmente en los colegios, en algún momento de la media, tienes que elegir como una ’especialización’ para tener más cursos enfocados en lo que se supone que vas a elegir como carrera después. El problema es que te hacen elegir cuando lo único que te importa es jugar fútbol, buscar polol@ o que tus papás no te molesten por salir a carretear. No estás muy pendiente de qué querrás hacer el resto de tu vida.
Así estaba yo a fines de segundo medio, cuando tenía que elegir a que electivo irme en el colegio, las opciones eran: el electivo humanista (lenguaje e historia), el científico (química, biología y física) o el matemático (matemáticas y física). Mi colegio ponía una psicopedagoga que se supone que te guiaba en esta elección, pero a mi me dijo “Tienes más o menos las mismas notas en todo ¿Qué te gusta más? Puedes elegir cualquiera de los 3 electivos”. Gracias por nada.
Mis dos hermanas eran humanistas y odiaban las matemáticas, así que con re poca confianza les copié y elegí el humanista. Así llegué a mi primera clase de lenguaje electivo el primer lunes de clases de tercero medio y la profe me preguntó “Anwar ¿Qué estás haciendo acá? Jamás pensé que estarías en el humanista”, el miércoles en la clase de historia, otra profe me dijo lo mismo así que empecé a cuestionarme si realmente debía estar ahí o no, pero como “me iba igual en todo” no sabía que hacer.
Dos semanas después decidí cambiarme y mi criterio fue bastante malo. En ese momento estaba pololeando con una niña que era seca en matemáticas así que me cambié al matemático, porque si algo me costaba, le iba poder preguntar a ella. 🙏🏽
SPOILER: Terminamos un par de meses después y no me ayudó mucho.
¿Cómo sobreviví al matemático sin ayuda?
Al principio me molestaron harto por cambiarme después de 2 semanas siendo humanista, pero afortunadamente, se me dió con mucha facilidad. Resultó que me gustó harto, lo encontraba desafiante y eso me motivaba a estudiar más y la verdad es que me iba mejor que varios de mis compañeros que habían tomado ese electivo como primera opción desde el principio.
Entonces desde ahí empecé a pensar si realmente las matemáticas son realmente difíciles o muchas personas solo se dejan llevar por lo que dicen los demás y no se esfuerzan lo suficiente por entender. Yo creo que no son para nada difíciles si logras darle una oportunidad real, tienes paciencia y un buen profe que te ayude.
Si no le das la oportunidad, es muy difícil que se te de fácil y siento que en muchísimos casos, eso es lo que pasa. De hecho, yo creo que muchos no van a leer este post solo porque dice matemáticas en el título.
La clave del éxito matemático definitivo
Hay algunas cosas que me he dado cuenta que funcionan para aprender matemáticas más rápido, fácil y entretenido (para derribar el mito de que son difíciles y fomes 💪🏼).
1. El profe debe hablar “tu mismo idioma”.
Una barrera enorme que se genera entre los profesores y estudiantes de matématicas es el lenguaje. En general, los profes de matemáticas son muy teorícos y te hablan de cosas raras como teoremas, algoritmos, abcisas y ordenadas. WTF!!???
Una técnica vital que fui agarrando con el tiempo es “traducir” lo que me enseñan en lenguaje matemático a lenguaje natural y cotidiano.
2. Hacerlo lo más entretenido que puedas.
Luego de que te hablan en un idioma raro, uno se suele desconcentrar. Pero si la clase fuera entretenida, estaría muchísimo más dispuesto a darle una segunda oportunidad y no dejaría de poner atención tan rápido.
Este es otro problema clásico de las clases de matemáticas. Son bastante fomes. Entonces cuando me hablaron de un teorema, que es una palabra que ni entiendo y más encima la clase es plana, no cambia de tono, solo explican cosas raras y rayan la pizarra con cosas que nunca voy a poder dibujar, me aburro y obviamente no pongo más atención.
Cuándo la clase es entretenida, es mucho más probable que esté más tiempo poniendo atención. Por lo tanto, es mucho más probable poder entender, querer participar o llegar a repasar después, porque lo asocio con un momento entretenido y no a un sufrimiento en el que me sentí tonto todo el rato por no entender.
3. Dejar la formalidad matemática y hacer que sea más entendible por todos (a pesar de que no sea tan correcto).
Parecido al punto 1, pero además de hablar en un idioma técnico difícil de entender, a la mayoría de los profesores de matemáticas que conozco, no les gusta mucho explicar las cosas como NO son. ¡Y está bien! No deberían enseñarnos cosas mal.
¿O si?
Para alguien que le cuestan las matemáticas, no creo que sea bueno seguir explicándole lo mismo de formas distintas, con lenguaje complicado y con todas las complejidades de la matemática ‘correcta’. Según yo, quién enseña debería ser capaz de enseñar de forma simplificada lo difícil. Al fin y al cabo, le estas tratando de enseñar algo que no le gusta mucho a alguien que probablemente no lo quiera usar en su día a día.
Claramente a quien si le interese y quiera dedicar su vida a la investigación, hay que enseñarle al pie de la letra, pero a una persona que solo quiere pasar un ramo, solo basta con enseñarle lo que necesita para entender la idea general y que lo pueda aplicar al contexto que lo necesite.
Muy pocas personas me han hablado sobre ecuaciones o teoremas en conversaciones cotidianas, así que para el común de los mortales una explicación no tan específica, no está tan mal si logra entenderlo y aplicarlo en un contexto donde no se requiere la teoría exacta.
Un ejemplo de todo esto combinado 🤞🏼
¿Sabías que una suma infinita de 0 no necesariamente es 0?
Voy a tratar de demostrarlo matemáticamente y que lo entiendas. Si estás dispuesto a aprender cosas entretenidas de matemática de primer año de U, puedes seguir leyendo. Si no te interesa, puedes saltarte todo hasta el siguiente título.
Todos sabemos que el área de un rectánculo es base * altura. ¿Pero que pasa si pensamos en una línea? Podríamos decir que esa línea es un rectángulo de base infinitamente chica (casi 0, por ejemplo 0,00000001 cm, pero puede ser tan chico como quieras, agregando más y más ceros) y altura igual al largo de la línea (por ejemplo 10 cm) tal como se muestra en la siguiente foto.
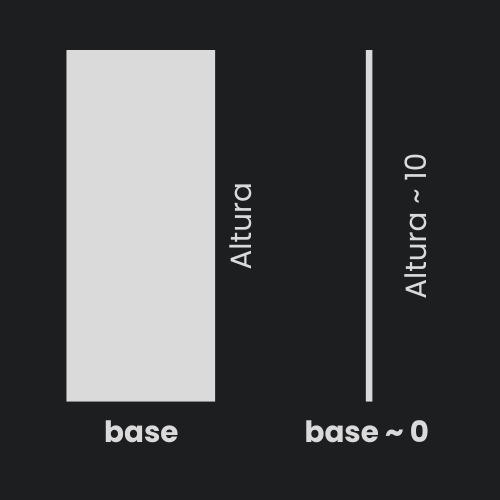
Entonces al calcular el área de esa línea/rectángulo (base * altura) sería algo muy cercano a 0 (0,00000001 cm * 10 cm = 0,0000001 cm2) así que podríamos decir que prácticamente es 0 ¿Cierto?.
¡Felicitaciones! Ahora sabes lo que es un límite. En general muchos sufren con esto el primer año de U.
Ahora imaginate dibujando muchísimos (millones) de estos rectángulos, que en verdad son líneas de largo 10 cm, justo uno al lado del otro, ultra pegados.

Después de un rato dibujando líneas vamos a lograr igualar la altura con la base, dibujando así un cuadrado tal como se ve aquí.
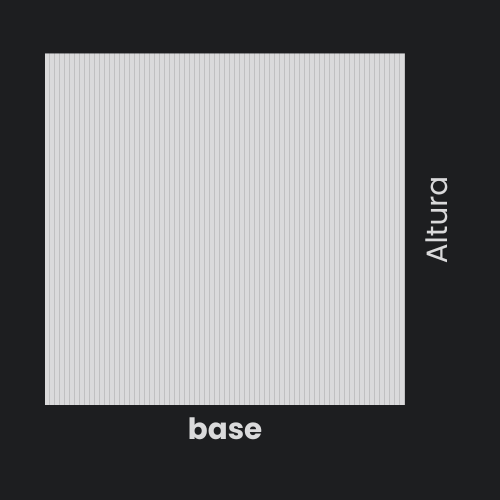
Pero espera… El área de un cuadrado, igual se calcula como base * altura y esa base no es 0 como la de las líneas que dibujamos al principio. De hecho, si es un cuadrado, la base es igual a la altura. Entonces dibujando solo líneas de área 0, puedo llegar a ‘pintar’ un cuadrado de área distinta de 0.
¡Exactamente! Sumar rectángulos de área 0, da un área mayor que 0, de hecho da 100 cm2 (10 cm * 10 cm).
Es decir, 0 + 0 + 0 + … + 0 no siempre es 0 🤯.
En este caso particular, 0 + 0 + 0 + … + 0 = 100. ¿Extraño no?
¡Felicitaciones nuevamente! Ahora sabes lo que es una integral. No es un logro menor, pensando que muchas personas no logran entenderlo el segundo semestre de una carrera con harta matemática.
La explicación de esto es que son cálculos de cosas ‘infinitamente’ chicas, entonces la matemática típica del colegio cambia un poco y pasan cosas raras como estas.
¿Qué es Pásalo 🚀?
Todo lo que expliqué acá lo fui aplicando cuando hacía clases a estudiantes de primer y segundo año en la U y la verdad es que varios de los estudiantes a los que les enseñé, me dijeron que les había ayudado mucho y terminamos siendo amigos, jugamos a la pelota y hasta el día de hoy hablamos. Muchos me siguen pidiendo clases, pero por temas de tiempo con la pega, no puedo ayudarlos mucho, así que junto a un amigo creamos una solución para ayudar a los estudiantes de primer año de ingeniería civil en la UAI puedan aprender y pasar sus ramos pasándolo bien en el proceso.
Esta solución se llama Pásalo y he estado trabajando en esto hace unos meses, porque confío en que un método más entretenido puede hacer que a los que les cuesta un poco seguirle el ritmo al profe, puedan tener buenas notas igual. El primer año es todo muy nuevo y muchas veces, si no recibes la ayuda necesaria, puede que te eches ramos y que por eso no sigas con tus amigos que te hiciste el primer semestre o que dudes si realmente elegiste la carrera que querías o no.
Estamos recién empezando, pero ya estamos ayudando a estudiantes para que se les haga un poco más ameno el inicio de año en una experiencia totalmente nueva para muchos. Así que si conoces alguien que esté en primer año de Ingeniería en la UAI (esperamos pronto ofrecerlo en más universidades y más carreras), contáctame para ayudarlo en sus primeras semanas como mechón!
Este ha sido uno de mis posts favoritos del blog! Si tienes algún comentario de este post o quieres hablarme para saber más de Pásalo, puedes escribirme por Instagram.
Si a ti también te gustó este post u otro del blog y quieres seguir leyendo más contenido como este, puedes suscribirte en el formulario de aquí abajo 👇🏼👇🏼👇🏼👇🏼.